Full Disk Simulations: Difference between revisions
| Line 20: | Line 20: | ||
9.24589, 10.24629, 11.24662, 12.24689, | 9.24589, 10.24629, 11.24662, 12.24689, | ||
13.24713, 14.24733, 15.24750]) | 13.24713, 14.24733, 15.24750]) | ||
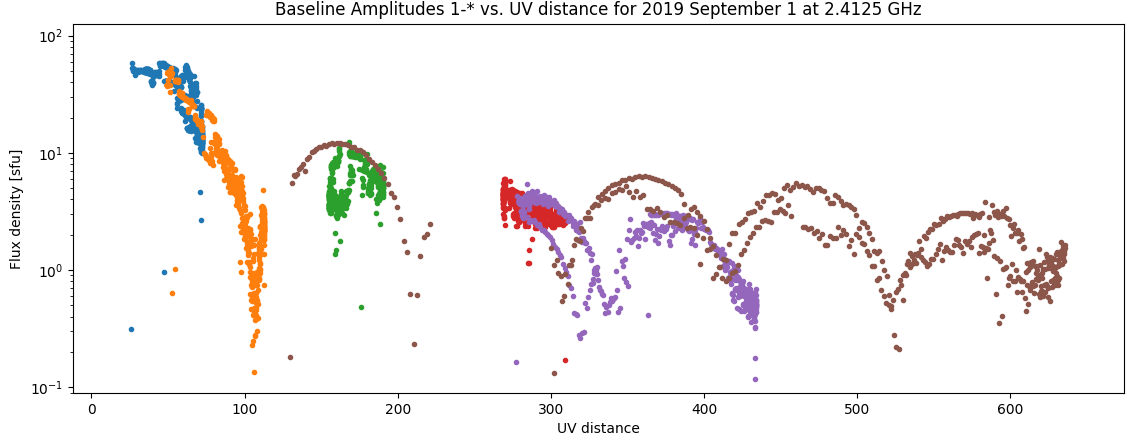
which must correspond to the nearly periodic dips (nulls) in Figure 1. | which must correspond to the nearly periodic dips (nulls) in Figure 1. The value of <math>z</math> is related to the diameter of the solar disk by the relation | ||
<math>D^{''} | <math>z = \pi D_{{\rm rad}} s_\lambda = \pi^2 D^{''}/(180\times3600) s_\lambda</math>, | ||
where <math>D_{{\rm rad}}</math> is the solar diameter in radians, <math>s_\lambda</math> is the uv distance in wavelengths, and the second relation is just the conversion to the solar diameter in arcsec, <math>D^{''}</math>. Note that the relevant disk size is not the photospheric radius, but rather the radius at radio frequencies, which varies with frequency and may even be different in the equatorial and polar axes. It may generally be expected to grow larger at lower frequencies, and grow more oblate near the equator as the coronal flux density becomes non-negligible. | |||
===Disk Fitting Python Code=== | |||
A set of three routines have been written in the Python module disk_fitting.py for the purposes of fitting the data in an all-day UDBms for the frequency-dependent disk shape and flux density. The input data are expected to be fully calibrated for amplitude and phase by the standard EOVSA pipeline. | |||
* The routine read_ms() reads the UDBms visibilities and returns the relevant data in a convenient dictionary format that is used by the subsequent fitting routines. This routine must be used in the CASA (or SunCASA) environment. Here is an example: | |||
import disk_fitting as df | |||
vis = '/data1/eovsa/fits/UDBms/201908/UDB20190825.ms' | |||
out = df.read_ms(vis) | |||
It takes several minutes to read an entire day's file. | |||
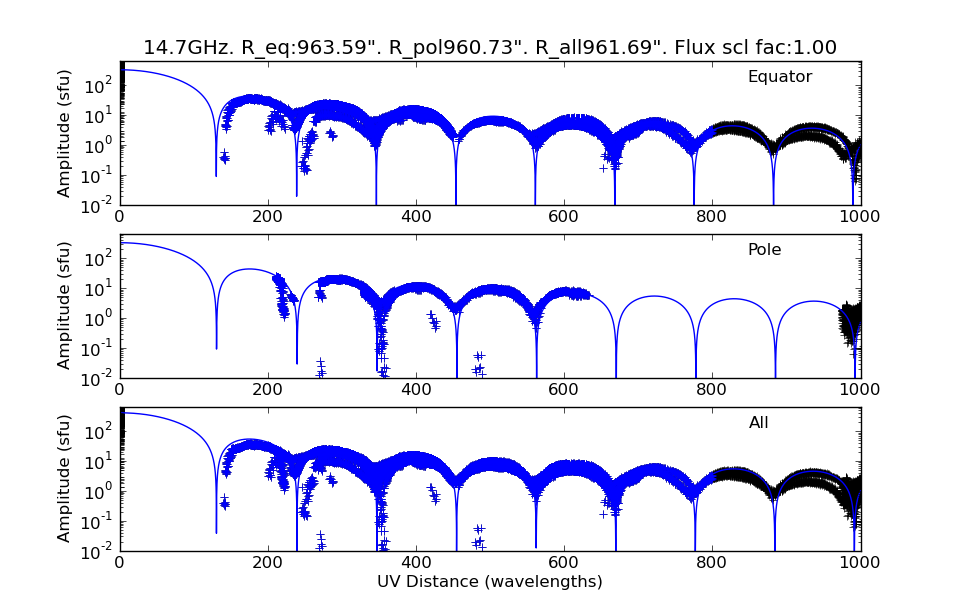
* The routine fit_diskmodel() uses the output from read_ms() and fits a disk model for one band (or spectral window, spw, in CASA parlance) at a time. A nice summary plot of the data and fit is generated if doplot=True. One thing that the routine needs is the full Sun flux density spectrum derived from the RSTN fluxes collected each day by NOAA. The example below shows how to get that information and use it to fit a disk to the spw 40 data using fit_diskmodel(): | |||
import rstn | |||
from util import Time | |||
frq, flux = rstn.rd_rstnflux(t=Time('2019-09-01')) | |||
rstn_flux = rstn.rstn2ant(frq, flux, out['fghz']*1000, t=Time('2019-09-01')) | |||
fit_diskmodel(out, 40, rstn_flux, uvfitrange=[20,800], angle_tolerance=np.pi/2) | |||
The resulting plot is shown in Figure 2, where the uv range used for fitting (20-800 wavelengths) is shown by the blue-highlighted data points. [[file:20190901_band40_diskfit.png|thumb|right|500px|'''Fig. 2:''' ]] | |||
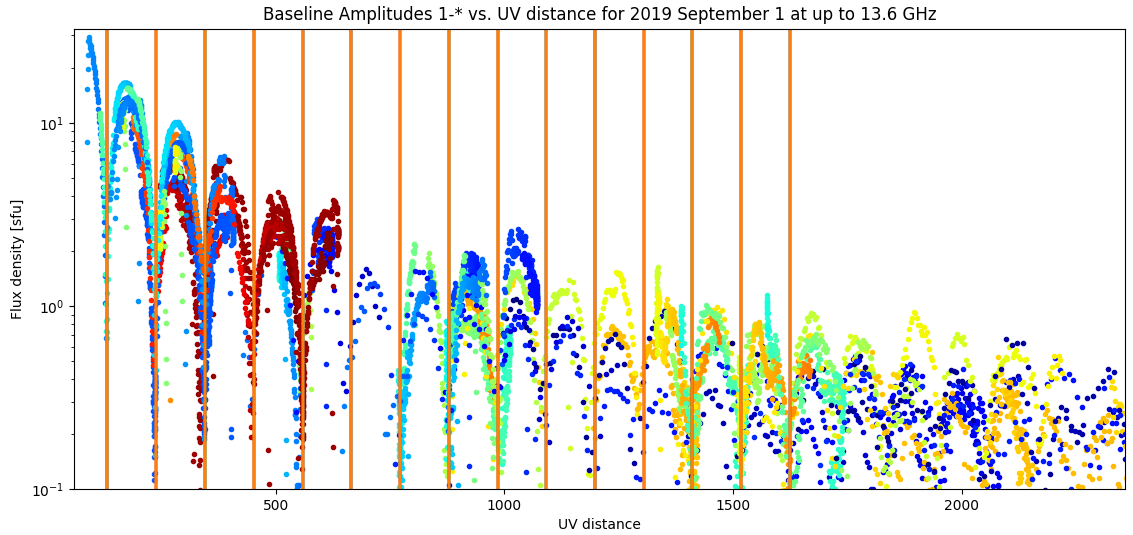
I also investigated whether there is a dependence on the location of the minima with the angle of the baseline (which would indicate a non-circular disk). There does seem to be some evidence for that, with a rather surprisingly large variation of order 10%. Still, the sizes I am getting for the equatorial direction are something like 2100", which is pretty big, so it might make sense that the polar direction is much smaller. One would expect these variations to decrease at higher frequency, where the disk is less affected by the corona. In fact, this does seem to be the case. Figure 2 shows the same date as Fig. 1, but at higher frequencies where a single radius (968") fits all of the nulls up to at least the first 15! Note that this is still 17" larger than the photospheric value of 951" on that date. [[file:Disk_vis_high_freq.png|thumb|right|500px|'''Fig. 2:''' Example all-day visibilities for baselines 1-* at frequencies around 10 GHz or higher, showing the periodic nulls due to the solar disk. The orange lines are the predicted position of the nulls for a disk of 968".]] | I also investigated whether there is a dependence on the location of the minima with the angle of the baseline (which would indicate a non-circular disk). There does seem to be some evidence for that, with a rather surprisingly large variation of order 10%. Still, the sizes I am getting for the equatorial direction are something like 2100", which is pretty big, so it might make sense that the polar direction is much smaller. One would expect these variations to decrease at higher frequency, where the disk is less affected by the corona. In fact, this does seem to be the case. Figure 2 shows the same date as Fig. 1, but at higher frequencies where a single radius (968") fits all of the nulls up to at least the first 15! Note that this is still 17" larger than the photospheric value of 951" on that date. [[file:Disk_vis_high_freq.png|thumb|right|500px|'''Fig. 2:''' Example all-day visibilities for baselines 1-* at frequencies around 10 GHz or higher, showing the periodic nulls due to the solar disk. The orange lines are the predicted position of the nulls for a disk of 968".]] | ||
Revision as of 00:49, 9 September 2019
Purpose
EOVSA's 13 antennas provide limited uv coverage for imaging the solar disk, but the baselines do contain considerable flux, especially on shorter baselines. We have good evidence that weak features of the quiet Sun (e.g. filament channels, prominences, and weak plage areas) do show up in the data, but the variations in brightness due to the poorly sampled disk often swamp them. The correct approach to imaging such features is to model the quiet solar disk and remove it from the uv data. then clean the residual flux that contains these weaker features, and finally add the disk model back. Self calibration also requires a good source model that includes the disk.
The purpose of this page is to describe the nuts and bolts of that procedure and document the performance.
NB: Since we are just getting started with this procedure, this page will initially present a number of tests. Ultimately it should become a definitive description of the procedure without a lot of false starts.
Creating Disk Models in CASA
The first step in simulating a source is to create a "sky model," which is an image and associated descriptive header information to represent a source in the sky. CASA's componentlist routines provide a recipe for creating different image components, including gaussian sources, point sources, disks, and so on. I created a python script diskmodel.py that eases the work of creating a disk model, which allows one to create a disk with unequal axes (generally larger in the equatorial axis and smaller in the polar axis). However, before it can be used one must have a good idea of the disk size and flux density of the disk.
Estimating disk axes and flux density from the data
One can use the data themselves to estimate the size of the disk needed to fit the data. As it turns out, EOVSA visibilities provide excellent measures of the disk shape and flux density if we can make use of it. After a lot of effort, I believe we have an understanding of how to interpret the EOVSA visibilities in terms of the disk shape and flux density, and therefore how to fit the data to derive estimates for the three key parameters: equatorial radius, polar radius, and flux density. In practice, the flux density seems to fit quite well with the flux density imposed by the total power/auto-correlation calibration, so it is likely that we will do better just using the nominal flux density imposed from RSTN. Figure 1 shows an example of some data for 2019 Sep 01.
The visibilities due to the solar disk are the same as the Fourier Transform of a circular aperture, which is an Airy pattern (not an Airy function, which apparently is a different mathematical function). The power distribution vs. radius in an Airy disk is , where is the first-order Bessel function and is the peak intensity. However, in the uv-plane we are looking not at the power, but rather the electric field pattern itself, hence we are interested in the square root of this function, i.e. . Note that the first 15 zeros of the airy disk are listed as:
m = array([ 1.21967, 2.23313, 3.23831, 4.24106,
5.24276, 6.24392, 7.24476, 8.24539,
9.24589, 10.24629, 11.24662, 12.24689,
13.24713, 14.24733, 15.24750])
which must correspond to the nearly periodic dips (nulls) in Figure 1. The value of is related to the diameter of the solar disk by the relation
,
where is the solar diameter in radians, is the uv distance in wavelengths, and the second relation is just the conversion to the solar diameter in arcsec, . Note that the relevant disk size is not the photospheric radius, but rather the radius at radio frequencies, which varies with frequency and may even be different in the equatorial and polar axes. It may generally be expected to grow larger at lower frequencies, and grow more oblate near the equator as the coronal flux density becomes non-negligible.
Disk Fitting Python Code
A set of three routines have been written in the Python module disk_fitting.py for the purposes of fitting the data in an all-day UDBms for the frequency-dependent disk shape and flux density. The input data are expected to be fully calibrated for amplitude and phase by the standard EOVSA pipeline.
- The routine read_ms() reads the UDBms visibilities and returns the relevant data in a convenient dictionary format that is used by the subsequent fitting routines. This routine must be used in the CASA (or SunCASA) environment. Here is an example:
import disk_fitting as df vis = '/data1/eovsa/fits/UDBms/201908/UDB20190825.ms' out = df.read_ms(vis)
It takes several minutes to read an entire day's file.
- The routine fit_diskmodel() uses the output from read_ms() and fits a disk model for one band (or spectral window, spw, in CASA parlance) at a time. A nice summary plot of the data and fit is generated if doplot=True. One thing that the routine needs is the full Sun flux density spectrum derived from the RSTN fluxes collected each day by NOAA. The example below shows how to get that information and use it to fit a disk to the spw 40 data using fit_diskmodel():
import rstn
from util import Time
frq, flux = rstn.rd_rstnflux(t=Time('2019-09-01'))
rstn_flux = rstn.rstn2ant(frq, flux, out['fghz']*1000, t=Time('2019-09-01'))
fit_diskmodel(out, 40, rstn_flux, uvfitrange=[20,800], angle_tolerance=np.pi/2)
The resulting plot is shown in Figure 2, where the uv range used for fitting (20-800 wavelengths) is shown by the blue-highlighted data points.
I also investigated whether there is a dependence on the location of the minima with the angle of the baseline (which would indicate a non-circular disk). There does seem to be some evidence for that, with a rather surprisingly large variation of order 10%. Still, the sizes I am getting for the equatorial direction are something like 2100", which is pretty big, so it might make sense that the polar direction is much smaller. One would expect these variations to decrease at higher frequency, where the disk is less affected by the corona. In fact, this does seem to be the case. Figure 2 shows the same date as Fig. 1, but at higher frequencies where a single radius (968") fits all of the nulls up to at least the first 15! Note that this is still 17" larger than the photospheric value of 951" on that date.