Full Disk Simulations: Difference between revisions
| (2 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
The first step in simulating a source is to create a "sky model," which is an image and associated descriptive header information to represent a source in the sky. CASA's [https://casaguides.nrao.edu/index.php/Simulation_Guide_Component_Lists_(CASA_5.4) componentlist] routines provide a recipe for creating different image components, including gaussian sources, point sources, disks, and so on. I created a python script diskmodel.py that eases the work of creating a disk model, but it remains too simple and will be embellished over time to create a more sophisticated disk. | The first step in simulating a source is to create a "sky model," which is an image and associated descriptive header information to represent a source in the sky. CASA's [https://casaguides.nrao.edu/index.php/Simulation_Guide_Component_Lists_(CASA_5.4) componentlist] routines provide a recipe for creating different image components, including gaussian sources, point sources, disks, and so on. I created a python script diskmodel.py that eases the work of creating a disk model, but it remains too simple and will be embellished over time to create a more sophisticated disk. | ||
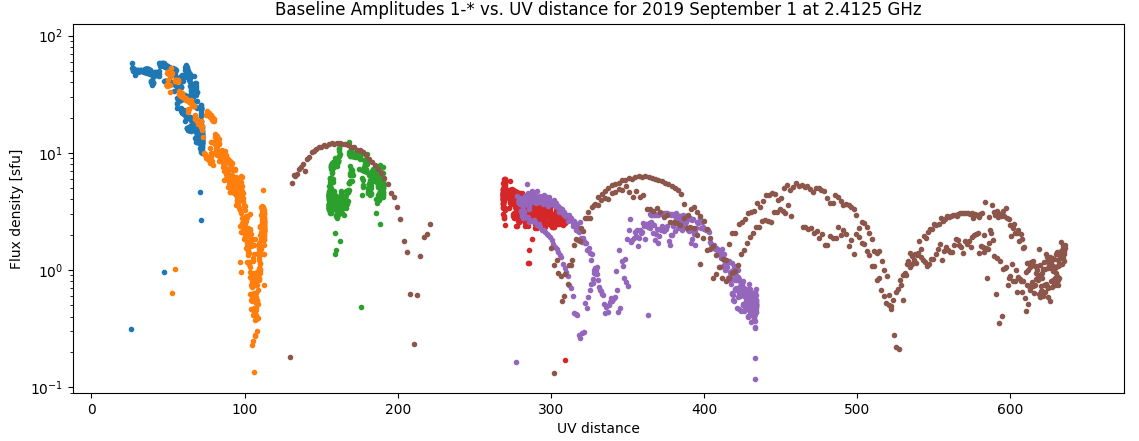
One can use the data themselves to estimate the size of the disk needed to fit the data. One suggestion is to use the zeros, or nulls, evident in the data. The first 15 zeros of the airy disk are listed as: | One can use the data themselves to estimate the size of the disk needed to fit the data. One suggestion is to use the zeros, or nulls, evident in the data. Figure 1 shows and example of some data for 2019 Sep 01. [[file:Disk_vis.png|thumb|right|500px|'''Fig. 1:''' Example all-day visibilities for baselines 1-*, showing the periodic nulls due to the solar disk.]] | ||
The first 15 zeros of the airy disk are listed as: | |||
m = array([ 1.21967, 2.23313, 3.23831, 4.24106, | m = array([ 1.21967, 2.23313, 3.23831, 4.24106, | ||
5.24276, 6.24392, 7.24476, 8.24539, | 5.24276, 6.24392, 7.24476, 8.24539, | ||
| Line 20: | Line 22: | ||
So the different minima will give different estimates and the final size would have to be some sort of mean of them. In some comparisons with the data, I do find that there is a systematic trend for the diameter to get smaller for larger ''m''. One possibility that I explored is whether a fuzzy disk has different minima than a sharply defined disk, but this does not seem to be the case. | So the different minima will give different estimates and the final size would have to be some sort of mean of them. In some comparisons with the data, I do find that there is a systematic trend for the diameter to get smaller for larger ''m''. One possibility that I explored is whether a fuzzy disk has different minima than a sharply defined disk, but this does not seem to be the case. | ||
I also investigated whether there is a dependence on the location of the minima with the angle of the baseline (which would indicate a non-circular disk). There does seem to be some evidence for that, with a rather surprisingly large variation of order 10%. Still, the sizes I am getting for the equatorial direction are something like 2100", which is pretty big, so it might make sense that the polar direction is much smaller. One would expect these variations to decrease at higher frequency, where the disk is less affected by the corona. | |||
Revision as of 20:34, 3 September 2019
Purpose
EOVSA's 13 antennas provide limited uv coverage for imaging the solar disk, but the baselines do contain considerable flux, especially on shorter baselines. We have good evidence that weak features of the quiet Sun (e.g. filament channels, prominences, and weak plage areas) do show up in the data, but the variations in brightness due to the poorly sampled disk often swamp them. The correct approach to imaging such features is to model the quiet solar disk and remove it from the uv data. then clean the residual flux that contains these weaker features, and finally add the disk model back. Self calibration also requires a good source model that includes the disk.
The purpose of this page is to describe the nuts and bolts of that procedure and document the performance.
NB: Since we are just getting started with this procedure, this page will initially present a number of tests. Ultimately it should become a definitive description of the procedure without a lot of false starts.
Creating Disk Models in CASA
The first step in simulating a source is to create a "sky model," which is an image and associated descriptive header information to represent a source in the sky. CASA's componentlist routines provide a recipe for creating different image components, including gaussian sources, point sources, disks, and so on. I created a python script diskmodel.py that eases the work of creating a disk model, but it remains too simple and will be embellished over time to create a more sophisticated disk.
One can use the data themselves to estimate the size of the disk needed to fit the data. One suggestion is to use the zeros, or nulls, evident in the data. Figure 1 shows and example of some data for 2019 Sep 01.
The first 15 zeros of the airy disk are listed as:
m = array([ 1.21967, 2.23313, 3.23831, 4.24106,
5.24276, 6.24392, 7.24476, 8.24539,
9.24589, 10.24629, 11.24662, 12.24689,
13.24713, 14.24733, 15.24750])
from which the diameter of the solar disk, in arcsec, is found from the location of the ith minimum, in uv wavelengths as
.
So the different minima will give different estimates and the final size would have to be some sort of mean of them. In some comparisons with the data, I do find that there is a systematic trend for the diameter to get smaller for larger m. One possibility that I explored is whether a fuzzy disk has different minima than a sharply defined disk, but this does not seem to be the case.
I also investigated whether there is a dependence on the location of the minima with the angle of the baseline (which would indicate a non-circular disk). There does seem to be some evidence for that, with a rather surprisingly large variation of order 10%. Still, the sizes I am getting for the equatorial direction are something like 2100", which is pretty big, so it might make sense that the polar direction is much smaller. One would expect these variations to decrease at higher frequency, where the disk is less affected by the corona.