Polarization Mixing Correction (Old): Difference between revisions
No edit summary |
|||
| Line 68: | Line 68: | ||
= Status of tests = | = Status of tests = | ||
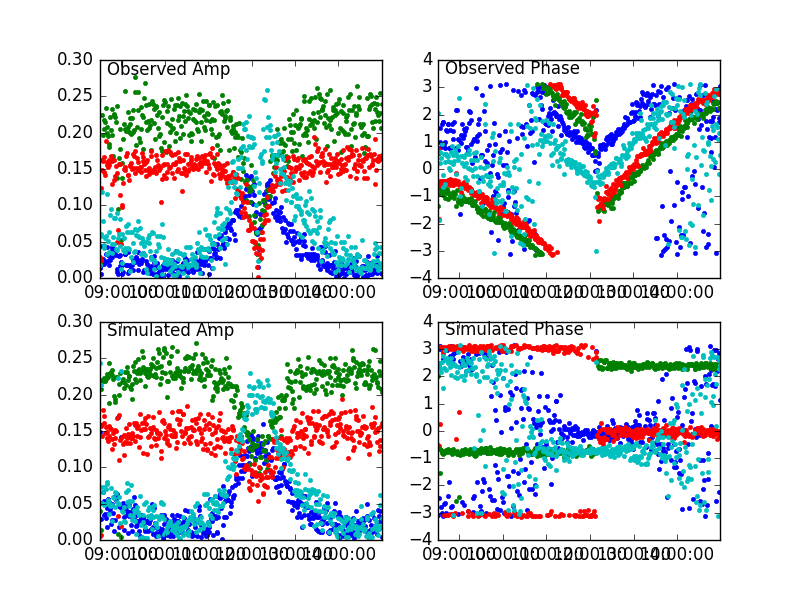
[[File: | [[File:3C84_no-rotation.png|thumb|400px|'''Fig. 3:''' Comparison of observed and simulated observations for 3C84 at a single frequency, while being tracked in hour angle. In all panels, XX = blue, XY = green, YX = red, and YY = cyan.]] | ||
To make the observations, we observe calibrator sources at different declincations over a broad range of hour angle. The two sources observed so far are 3C84, at declination 41 degrees, and 3C273, at declination 2 degrees. We then plot the observed amplitude and phase for each of the observed polarization products [XX, XY, YX, YY]. For this demonstration, we will use the baseline of Ant1-14, where Ant1 is the rotating feed and Ant14 is the non-rotating one (with respect to the celestial coordinate system). '''Figure 3''' shows | To make the observations, we observe calibrator sources at different declincations over a broad range of hour angle. The two sources observed so far are 3C84, at declination 41 degrees, and 3C273, at declination 2 degrees. We then plot the observed amplitude and phase for each of the observed polarization products [XX, XY, YX, YY]. For this demonstration, we will use the baseline of Ant1-14, where Ant1 is the rotating feed and Ant14 is the non-rotating one (with respect to the celestial coordinate system). '''Figure 3''' shows the 3C84 observation and simulation. The upper-left panel is the observed amplitude of the four polarization products during an observation from 08:30-15:00 UT, and the upper-right panel is the corresponding phase. The lower panels are the simulation amplitude and phase, where the simulation assumed constant polarization products with Amp[XX, XY, YX, YY] = [0.15, 0, 0, 0.23], and Phase[XX, XY, YX, YY] = [3.1, 0, 0, 2.4] (radians). A noise level of 0.015 rms was added. It is clear that the amplitude simulation works very well, but the phase does not have the correct character. As a test, | ||
Revision as of 17:46, 21 October 2016
Explanation of Polarization Mixing
The newer 2.1-m antennas [Ants 1-8 and 12] have AzEl (azimuth-elevation) mounts (also referred to as AltAz; the terms Altitude and Elevation are used synonymously), which means that their crossed linear feeds have a constant angle relative to the horizon (the axis of rotation being at the zenith). The older 2.1-m antennas [Ants 9-11 and 13], and the 27-m antenna [Ant 14], have Equatorial mounts, which means that their crossed linear feeds have a constant angle with respect to the celestial equator, the axis of rotation being at the north celestial pole. Thus, the celestial coordinate system is tilted by the local co-latitude (complement of the latitude). This tilt results in a relative feed rotation between the 27-m antenna and the AzEl mounts, but not between the 27-m and the older equatorial mounts. This angle is called the "parallactic angle," and is given by:
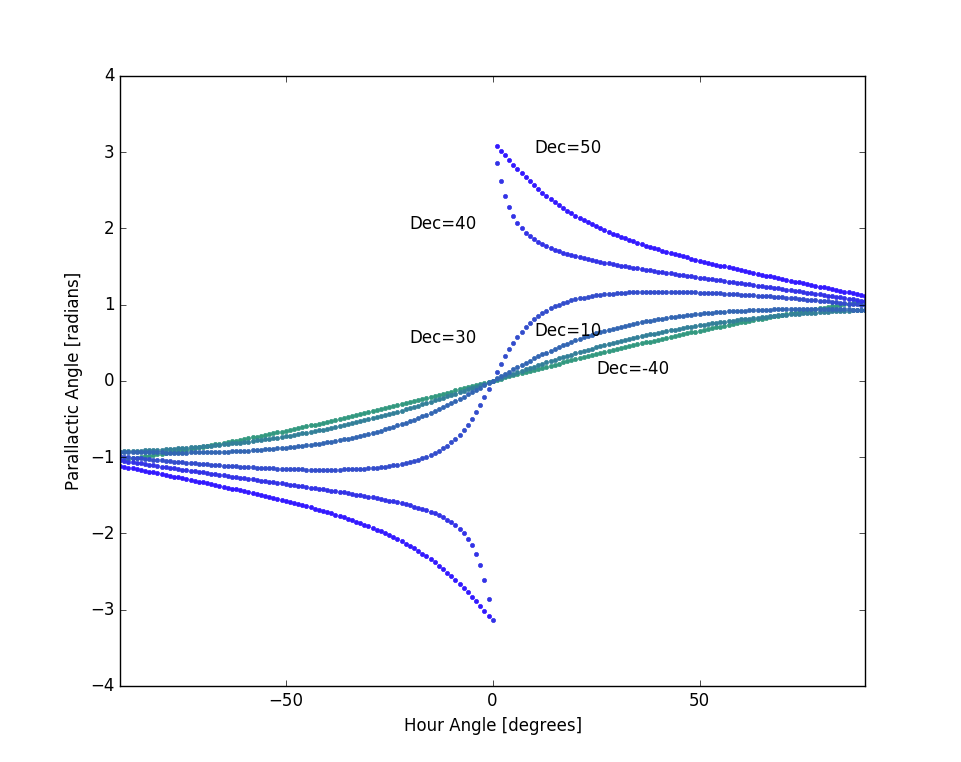
where is the site latitude, is the Azimuth angle [0 north], and is the Elevation angle [0 on horizon]. This function obviously changes with position on the sky, and as we follow a celestial source (e.g. the Sun) across the sky this rotation angle is continuously changing in a surprisingly complex manner as shown in Figure 1. Note that at zero hour angle for declinations less than the local latitude (37.233 degrees at OVRO), but is at higher declinations.
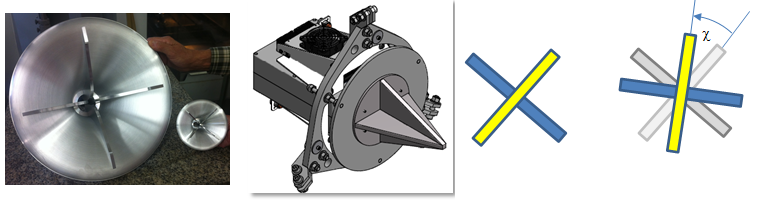
The crossed linear dipole feeds on all antennas are oriented with the X-feed as shown in Figure 2, at 45-degrees from the horizontal, when the antenna is pointed at 0 hour angle. This is the view as seen looking down at the feed from the dish side, although since the feeds are at the prime focus this is the same as the view projected onto the sky. At other positions, the feeds on the AzEl antennas experience a rotation by angle relative to the equatorial antennas.
Because of this rotation, the normal polarization products XX, XY, YX and YY on baselines with dissimilar antennas (one AzEl and the other equatorial) become mixed. The effect of this admixture can be written by the use of Jones matrices (see Hamaker, Bregman & Sault (1996) for a complete description). Consider antenna A whose feed orientation is rotated by , cross-correlated with antenna B with unrotated feed. The corresponding Jones matrices, acting on signal vector are:
and the cross-correlation is found by taking the outer product, i.e.
which relates the output polarization products to the input as
where we have dropped the subscripts and complex conjugate notation for brevity. Of course, there are other effects such as unequal gains and cross-talk between feeds that are also at play, but for now we ignore those and focus only on the effect of this polarization mixing due to the parallactic angle.
Ultimately we will apply the inverse of the above matrix to the measure polarization products to recover the unrotated polarization products, but for now we will content ourselves with demonstrating, in the next section, that we have the correct expressions by comparing observations with simulations.
Status of tests
To make the observations, we observe calibrator sources at different declincations over a broad range of hour angle. The two sources observed so far are 3C84, at declination 41 degrees, and 3C273, at declination 2 degrees. We then plot the observed amplitude and phase for each of the observed polarization products [XX, XY, YX, YY]. For this demonstration, we will use the baseline of Ant1-14, where Ant1 is the rotating feed and Ant14 is the non-rotating one (with respect to the celestial coordinate system). Figure 3 shows the 3C84 observation and simulation. The upper-left panel is the observed amplitude of the four polarization products during an observation from 08:30-15:00 UT, and the upper-right panel is the corresponding phase. The lower panels are the simulation amplitude and phase, where the simulation assumed constant polarization products with Amp[XX, XY, YX, YY] = [0.15, 0, 0, 0.23], and Phase[XX, XY, YX, YY] = [3.1, 0, 0, 2.4] (radians). A noise level of 0.015 rms was added. It is clear that the amplitude simulation works very well, but the phase does not have the correct character. As a test,







![{\displaystyle {\boldsymbol {e}}_{in}=[X,Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc4eeebe0b92120f842f54a160b57734dc5f6b5e)