Total Power Calibration: Difference between revisions
No edit summary |
No edit summary |
||
| Line 41: | Line 41: | ||
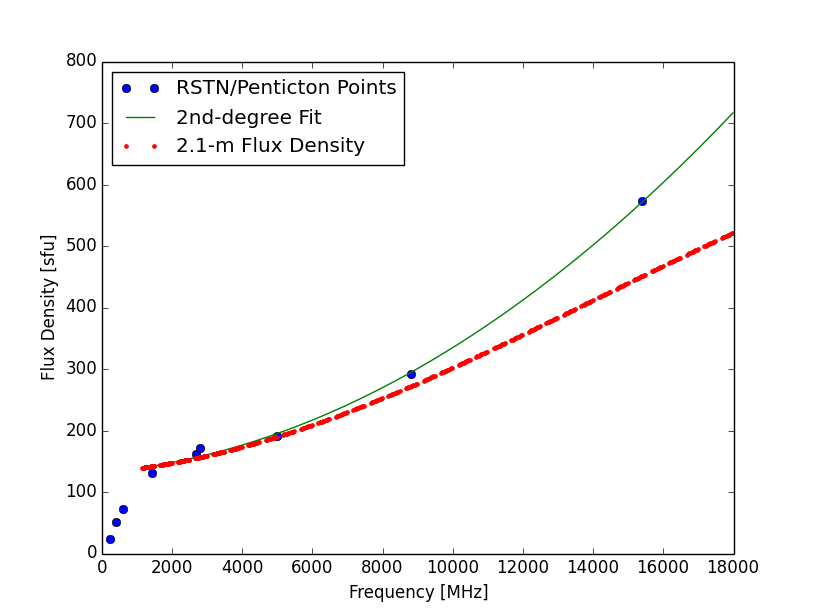
Obviously, this table cannot be completed until after a particular day’s observations are done (typically around 0300 UT on the following day), although Learmonth and San Vito data are available at the start of EOVSA’s observing day. Therefore, a real-time calibration of data must be a preliminary one based only on those two stations. The calibration should be redone overnight after more complete information has become available. Although these multiple flux density measurements could differ due to actual changes in solar flux density over the day, differences are generally small and this effect is ignored. The set of points is reduced to a single spectrum by taking the median of multiple values (where they occur). These measurements at a few discrete frequencies must then be both interpolated and extrapolated onto EOVSA’s frequencies. When such discrete frequency points are plotted, it is easy to see that points below 1.4 GHz do not follow a frequency-squared law (see blue points in Fig. 1). | Obviously, this table cannot be completed until after a particular day’s observations are done (typically around 0300 UT on the following day), although Learmonth and San Vito data are available at the start of EOVSA’s observing day. Therefore, a real-time calibration of data must be a preliminary one based only on those two stations. The calibration should be redone overnight after more complete information has become available. Although these multiple flux density measurements could differ due to actual changes in solar flux density over the day, differences are generally small and this effect is ignored. The set of points is reduced to a single spectrum by taking the median of multiple values (where they occur). These measurements at a few discrete frequencies must then be both interpolated and extrapolated onto EOVSA’s frequencies. When such discrete frequency points are plotted, it is easy to see that points below 1.4 GHz do not follow a frequency-squared law (see blue points in Fig. 1). | ||
[[File:RSTN.png| | <center>[[File:RSTN.png|600px|frame|Fig. 1: Flux density points from 2014 Nov. 26 (the above table), together with 2nd-degree polynomial fit and adjustment for 2.1-m dish primary beam.]]</center> | ||
Revision as of 00:51, 5 August 2016
EOVSA Total Power Calibration Method, Observations, and Analysis
The current EOVSA system should now be amenable to total power calibration based on RSTN/Penticton total solar flux density measurements. The outline of the method is to read the daily flux density measurements available from NOAA (e.g. [1]), calculate a suitable mean value for the multiple measurements made during the day, apply a second-order fit for interpolation/extrapolation to the EOVSA frequencies (), and then adjust the flux density to account for the finite size of the EOVSA (2.1-m diameter) antennas. Once this as-observed flux density spectrum is known, the results of daily SOLPNTCAL observations are used to determine the on-Sun spectrum for antenna , polarization , , and off-Sun spectrum for antenna , polarization , . The resulting calibration factors for antenna are determined as
To apply to some observed measurements on a particular antenna , to obtain the calibrated total power values , the calculation is:
This analysis ignores any change in gain (or attenuation) between the SOLPNTCAL measurement of the solar increment and the observed measurements to which it is applied. Gain calibration is a separate issue that will be described in another document.
1. SOLPNTCAL Pointing Calibration
This is based primarily on the scheme developed for KSRBL (Dou et al. 2009, PASP, 121, 512). The pointing offsets for all antennas can be determined simultaneously, and as a function of frequency, by offsetting each antenna in a cross pattern and measuring the total power spectrum. This provides multiple useful parameters: (i) frequency-dependent pointing offsets, which can be surprisingly large, and are necessary for primary beam corrections to all interferometer amplitudes, (ii) direct measurement of the primary beam size and shape, and (iii) a check on overall total power gain calibration relative to that determined interferometrically on cosmic sources.
This type of pointing can be done quickly (the observation takes 5 minutes for EOVSA) and is done twice daily (in case one of the observations is not successful). A special antenna control sequence (trajectory) has been implemented, which points a maximum of 5 degrees off Sun in a cross pattern. The current offset sequence in degrees is
- RAO = -5.0,-2.0,-1.0,-0.5,-0.2,-0.1, 0.0, 0.1, 0.2, 0.5, 1.0, 2.0, 5.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0
- DECO= 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,-5.0,-2.0,-1.0,-0.5,-0.2,-0.1, 0.0, 0.1, 0.2, 0.5, 1.0, 2.0, 5.0
where RAO must be divided by cos(Dec) to convert to a plane-of-the-sky offset.
2. RSTN Flux Density Database
The daily RSTN/Penticton flux density measurements reported by NOAA are taken at 9 frequencies, with four measurements per day at 8 frequencies from RSTN stations and three per day (generally) from Penticton at 2800 MHz (F10.7).
Below is a typical example (missing data is flagged with -1):
2014 Nov 26 245 24 27 24 -1 -1 20 -1 410 44 55 50 -1 -1 51 -1 610 70 -1 73 -1 -1 79 -1 1415 130 131 117 -1 -1 131 -1 2695 160 163 162 -1 -1 157 -1 2800 -1 -1 -1 169 171 -1 171 4995 190 191 188 -1 -1 202 -1 8800 246 299 284 -1 -1 315 -1 15400 551 605 475 -1 -1 594 -1
Obviously, this table cannot be completed until after a particular day’s observations are done (typically around 0300 UT on the following day), although Learmonth and San Vito data are available at the start of EOVSA’s observing day. Therefore, a real-time calibration of data must be a preliminary one based only on those two stations. The calibration should be redone overnight after more complete information has become available. Although these multiple flux density measurements could differ due to actual changes in solar flux density over the day, differences are generally small and this effect is ignored. The set of points is reduced to a single spectrum by taking the median of multiple values (where they occur). These measurements at a few discrete frequencies must then be both interpolated and extrapolated onto EOVSA’s frequencies. When such discrete frequency points are plotted, it is easy to see that points below 1.4 GHz do not follow a frequency-squared law (see blue points in Fig. 1).






![{\displaystyle c(p,f,i)=s(f)/[S_{on}(p,f,i)-S_{off}(p,f,i)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7652a61a785c7cc7ba37086ed28bde946af3ffb4)


![{\displaystyle T(p,f,i)=[o(p,f,i)-S_{off}(p,f,i)]\times c(p,f,i)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50f40e76f5bf760687971f2febece3648631a2f5)