Polarization Mixing Correction (Old): Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
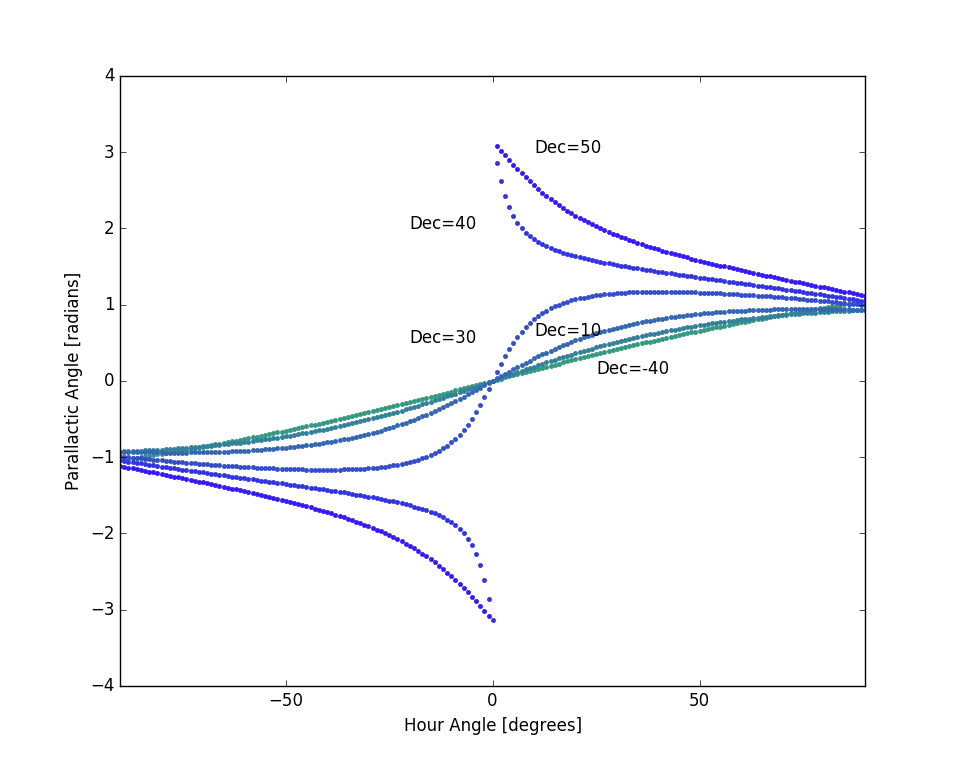
[[File:parallactic.png|thumb|400px|Fig. 1: Parallactic angle for a range of hour angle and declination. There is a large deviation for sources whose Dec = latitude (37 degrees), when they pass directly overhead.]] | |||
= Explanation of Polarization Mixing = | = Explanation of Polarization Mixing = | ||
The newer 2.1-m antennas [Ants 1-8 and 12] have AzEl (azimuth-elevation) mounts (also referred to as AltAz, where Altitude and Elevation are used synonymously), which means that their crossed linear feeds have a constant angle relative to the horizon (the axis of rotation being at the zenith). The older 2.1-m antennas [Ants 9-11 and 13], and the 27-m antenna [Ant 14], have Equatorial mounts, which means that their crossed linear feeds have a constant angle with respect to the celestial equator, the axis of rotation being at the north celestial pole. Thus, the celestial coordinate system is tilted by the local co-latitude (complement of the latitude). This tilt results in a relative feed rotation between the 27-m antenna and the AzEl mounts, but not between the 27-m and the older equatorial mounts. This angle is called the "parallactic angle," and is given by: | The newer 2.1-m antennas [Ants 1-8 and 12] have AzEl (azimuth-elevation) mounts (also referred to as AltAz, where Altitude and Elevation are used synonymously), which means that their crossed linear feeds have a constant angle relative to the horizon (the axis of rotation being at the zenith). The older 2.1-m antennas [Ants 9-11 and 13], and the 27-m antenna [Ant 14], have Equatorial mounts, which means that their crossed linear feeds have a constant angle with respect to the celestial equator, the axis of rotation being at the north celestial pole. Thus, the celestial coordinate system is tilted by the local co-latitude (complement of the latitude). This tilt results in a relative feed rotation between the 27-m antenna and the AzEl mounts, but not between the 27-m and the older equatorial mounts. This angle is called the "parallactic angle," and is given by: | ||
| Line 6: | Line 8: | ||
where <math>\lambda</math> is the site latitude, <math>A</math> is the Azimuth angle [0 north], and <math>E</math> is the Elevation angle [0 on horizon]. This function obviously changes with position on the sky, and as we follow a celestial source (e.g. the Sun) across the sky this rotation angle is continuously changing in a surprisingly complex manner. | where <math>\lambda</math> is the site latitude, <math>A</math> is the Azimuth angle [0 north], and <math>E</math> is the Elevation angle [0 on horizon]. This function obviously changes with position on the sky, and as we follow a celestial source (e.g. the Sun) across the sky this rotation angle is continuously changing in a surprisingly complex manner. | ||
= Status of tests = | = Status of tests = | ||
Revision as of 20:47, 20 October 2016
Explanation of Polarization Mixing
The newer 2.1-m antennas [Ants 1-8 and 12] have AzEl (azimuth-elevation) mounts (also referred to as AltAz, where Altitude and Elevation are used synonymously), which means that their crossed linear feeds have a constant angle relative to the horizon (the axis of rotation being at the zenith). The older 2.1-m antennas [Ants 9-11 and 13], and the 27-m antenna [Ant 14], have Equatorial mounts, which means that their crossed linear feeds have a constant angle with respect to the celestial equator, the axis of rotation being at the north celestial pole. Thus, the celestial coordinate system is tilted by the local co-latitude (complement of the latitude). This tilt results in a relative feed rotation between the 27-m antenna and the AzEl mounts, but not between the 27-m and the older equatorial mounts. This angle is called the "parallactic angle," and is given by:
where is the site latitude, is the Azimuth angle [0 north], and is the Elevation angle [0 on horizon]. This function obviously changes with position on the sky, and as we follow a celestial source (e.g. the Sun) across the sky this rotation angle is continuously changing in a surprisingly complex manner.